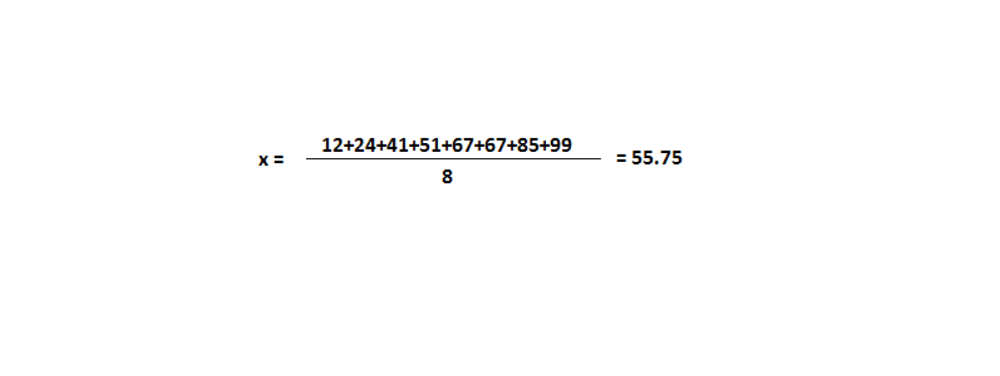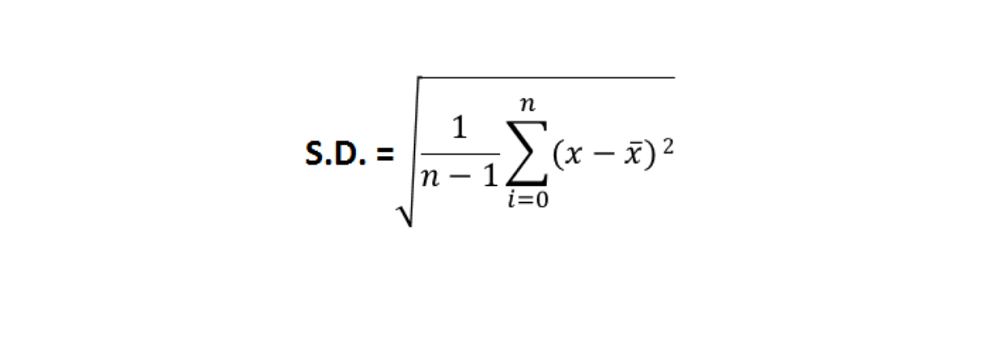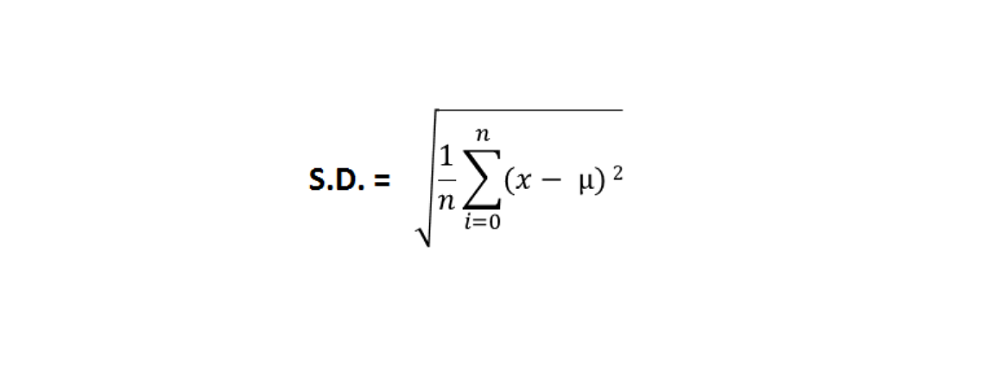آمار توصیفی (Descriptive Statistics) چیست؟

آمار شاخه‌ای از ریاضیات است که با جمع‌آوری، سازماندهی و تفسیر داده‌ها سروکار دارد. در ابتدا وقتی داده‌ها را به دست می‌آوریم، به‌جای استفاده از الگوریتم‌های فانتزی و برخی پیش‌بینی‌ها، سعی می‌کنیم داده‌ها را با استفاده از تکنیک‌های آماری بخوانیم و درک کنیم. با این کار می‌توانیم بفهمیم داده‌های توزیع شده، از چه نوع هستند. در متن پیش رو این مهم را بیشتر بررسی خواهیم کرد.

آمار توصیفی (Descriptive Statistics) چیست؟

آمار توصیفی شامل جمع‌بندی و سازماندهی داده‌ها است تا بتوان آن‌ها را به راحتی درک کرد. آمار توصیفی، برخلاف آمار استنباطی (Inferential Statistics)، به دنبال توصیف داده‌ها است، اما سعی در نتیجه‌گیری از نمونه به کل جمعیت ندارد. این امر به طور کلی به این معنی است که آمار توصیفی، برخلاف آمار استنباطی، بر اساس تئوری احتمال توسعه نمی‌یابد.

انواع آمار توصیفی

آمار توصیفی به دو دسته تقسیم می‌شود. معیار تمایل مرکزی و اندازه‌گیری‌های گسترش. هر کدام از این موارد زیرمجموعه‌های خود را دارند که در ادامه توضیح خواهیم داد.

۱- معیار تمایل مرکزی

فرض کنید یک عدد وجود دارد که به طور کامل، کل مجموعه اندازه‌گیری‌ها را خلاصه می‌کند، عددی که به نوعی “مرکزی” برای مجموعه است. این مهم تمام معنای معیار تمایل مرکزی را در خود دارد.

• میانگین / متوسط

میانگین نشان‌دهنده میزان تمایل اصلی داده‌ها است. یعنی تعدادی که کل داده‌ها در اطراف آن پخش می‌شوند. به نوعی، این یک عدد واحد است که می‌تواند مقدار کل مجموعه داده را تخمین بزند. برای درک بهتر این موضوع، می‌توانیم میانگین مجموعه داده‌های دارای ۸ عدد صحیح را محاسبه کنیم.

• میانه

میانه مقداری است که داده‌ها را به ۲ قسمت مساوی تقسیم می‌کند. یعنی تعداد اصطلاحات در سمت راست آن همانند تعدادی اصطلاحات سمت چپ آن است. همچنین داده‌ها به ترتیب صعودی یا نزولی مرتب می‌شوند. اگر داده‌ها را به ترتیب نزولی مرتب کنید، بر میانگین تأثیر نمی‌گذارد اما ضریب عدد، منفی خواهد بود. اگر تعداد اصطلاحات عددی فرد باشد، میانه میان‌مدت خواهد بود و اگر تعدادی از اصطلاحات یکنواخت باشد، میانگین ۲ اصطلاح میانی خواهد بود. برای نمونه:

۵۹=۹۹+۸۵+۶۷+۶۷+۵۱+۴۱+۲۴+۱۲

در این مثال، میانه ۵۹ است که مجموعه‌ای از اعداد را به دو قسمت مساوی تقسیم می‌کند. از آنجا که در مجموعه اعداد زوج وجود دارد، پاسخ میانگین اعداد میانی ۵۱ و ۶۷ است. توجه داشته باشید که وقتی مقادیر در حال پیشرفتِ حساب هستند (اختلاف بین اصطلاحات متوالی ثابت و در اینجا عدد ۲ است)، میانگین همیشه برابر با میانگین می‌باشد. بدون اعداد ۲,۴,۶,۸,۱۰، میانگین و همین‌طور میانه اعداد، عدد ۶ ​​است.

• حالت

اصطلاحی است که با توجه به آن حداکثر زمان در مجموعه داده‌ها نشان داده می‌شود. یعنی اصطلاحی که بیشترین تکرر را دارد.

۱۲,۲۴,۴۱,۵۱,۶۷,۶۷,۸۵,۹۹

در این مجموعه داده، حالت ۶۷ است زیرا بیش از بقیه مقادیر یعنی دوبرابر می‌باشد. این امکان نیز وجود دارد که یک مجموعه داده داشته باشیم که هیچ حالتی در آن نباشد. زیرا همه مقادیر به‌دفعات یکسان نشان داده می‌شوند. اگر دو مقدار به‌طور هم زمان و بیشتر از بقیه مقادیر ظاهر شوند، مجموعه داده دوحالته (Bimodal) است. اگر سه مقدار به طور هم زمان و بیشتر از بقیه مقادیر ظاهر شوند، مجموعه داده سه‌حالته (Trimodal) و برای n حالت، مجموعه داده چندحالته (Multimodal) است.

۲- اندازه‌گیری گسترش / پراکندگی

اندازه‌گیری‌های تغییر و یا گسترش (Measure of Spread)، به ایده تغییرپذیری داده‌ها اشاره دارد.

• انحراف معیار

انحراف معیار (Standard Deviation یا SD) اندازه‌گیری میانگین فاصله بین هر کمیت و میانگین است. یعنی نحوه انتشار داده‌ها از میانگین. انحراف استاندارد پایین نشان می‌دهد که نقاط داده به میانگین مجموعه داده نزدیک هستند، در حالی که انحراف استاندارد بالا نشان می‌دهد که نقاط داده در محدوده وسیع‌تری از مقادیر پراکنده شده‌اند.

گاهی شرایطی پیش می‌آید که ما باید بین نمونه یا جمعیت انحراف معیار، یکی را انتخاب کنیم. وقتی از ما خواسته می‌شود انحراف معیار بخشی از جمعیت را پیدا کنیم، ما از نمونه انحراف استاندارد استفاده می‌کنیم که در آن x̅ میانگین یک نمونه است.

اما وقتی باید با کل جمعیت سروکار داشته باشیم، از انحراف معیار جمعیت استفاده می‌کنیم. جایی که μ میانگین یک جمعیت است.

اگرچه نمونه بخشی از جمعیت است و انتظار می‌رود فرمول‌های SD آن‌ها باید یکسان باشد، اما این‌طور نیست. همان‌طور که می‌دانید، در آمار توصیفی، ما به طور کلی با داده‌های موجود در یک نمونه سروکار داریم، نه در یک جمعیت. بنابراین اگر از مجموعه داده‌های قبلی استفاده کنیم و مقادیر موجود در فرمول را جایگزین کنیم،

نتیجه سخن

امروزه، کلان داده به کلمه کلیدی در دنیای علم داده تبدیل شده است. این امر به طور گسترده مورد تحقیق قرار می‌گیرد و باعث می‌شود که داده‌ها پردازش و با دقت بررسی شوند. یکی از تکنیک‌های تجزیه‌وتحلیل این داده‌ها، آمار توصیفی است. در متن پیش رو سعی کردیم این مسئله را به طور مفصل مورد توجه قرار دهیم تا حساسیت آن برای شما قابل درک باشد.